LIQUIDE (ÉTAT)

LIQUIDE (ÉTAT)

La notion de liquide est une notion familière, l’état liquide étant, avec l’état solide et l’état gazeux, l’un des trois états communs de la matière.

On peut étudier un liquide comme une phase condensée fluide. Cela signifie que le liquide a une masse spécifique élevée, proche de celle du solide, et qu’il est aisément déformable, au point d’adapter sa forme à celle des récipients dans lesquels il est placé, contrairement au solide. L’existence d’une tension superficielle confère aux liquides des propriétés spécifiques, comme les phénomènes capillaires.

À l’échelle de l’atome ou de la molécule, un liquide se révèle être une phase compacte partiellement désordonnée. Les propriétés des liquides dépendent fortement de la façon dont l’énergie d’interaction de deux molécules varie avec leur orientation et leur distance relatives. Dans les cas extrêmes, on peut voir apparaître des propriétés particulières, comme celles de cristal liquide.

1. La phase liquide

En général, dans le cas d’un corps pur, le changement d’état, c’est-à-dire le passage du solide au liquide ou du liquide au gaz, intervient à une température fixe qui reste constante tant que les deux phases sont en présence et qui ne varie qu’avec la pression.

Ces changements d’états sont réversibles. En l’absence de phénomènes parasites (surfusion), la fusion du solide se produit à la même température (point de fusion) que la solidification du liquide (point de solidification). De même, le point d’ébullition ou de vaporisation du liquide et le point de condensation du gaz sont identiques. La quantité de chaleur mise en jeu dans ces transformations, appelée chaleur latente du changement de phase considéré, est égale, au signe près, dans les transformations inverses. La fusion et la vaporisation sont des phénomènes endothermiques, alors que la solidification et la condensation sont exothermiques.

La variation de la pression sous laquelle se fait un changement d’état à température donnée est représentée sur le diagramme (p , T) de la figure 1. On y remarque un point triple qui correspond au point de coexistence des phases solide, liquide et gaz. À des températures ou à des pressions inférieures à celles du point triple, le liquide n’existe plus, et si un solide est chauffé à une pression inférieure à la pression du point triple, il se transforme directement en gaz (sublimation). De même, on peut constater que la courbe représentant les points d’ébullition s’arrête brusquement pour une certaine température, dite critique (T^c), au-dessus de laquelle il n’existe qu’une phase fluide. Au voisinage du point critique, la distinction entre liquide et gaz est donc relativement floue.

La distinction entre liquide et solide peut, elle aussi, être beaucoup moins nette qu’on le pense de prime abord. Il arrive en effet que, par abaissement de température, la fluidité du liquide diminue de façon importante et que l’on passe progressivement du liquide à un corps pâteux puis à un solide, que l’on qualifie alors de vitreux. C’est le cas du verre, ce qui permet son travail sous forme pâteuse, ainsi que de nombreuses matières plastiques (thermoplastiques) et de certains liquides moléculaires comme l’alcool éthylique (éthanol).

2. Les propriétés des liquides

Si l’on excepte de très rares cas particuliers, comme l’eau (cf. chap. 3), tous les corps subissent à la fusion une augmentation de volume de 5 à 15 p. 100. La masse spécifique d’un liquide diffère donc assez peu de celle de la même substance à l’état solide et, près du point de fusion, la compressibilité du liquide n’est que peu supérieure à celle du solide. De même, la chaleur latente de fusion est toujours nettement inférieure à la chaleur latente d’ébullition. Ces faits indiquent que certaines grandeurs physiques sont peu différentes à l’état liquide et à l’état solide. Mais les liquides ont des propriétés tout à fait caractéristiques, comme la fluidité, ou sa grandeur inverse la viscosité, et les phénomènes de tension superficielle.

La viscosité des liquides

La grandeur qui mesure la résistance d’un liquide à l’écoulement, appelée viscosité, est définie par la loi de Poiseuille. D’après cette loi, le débit volumique d V/dt d’un fluide, dans un tube cylindrique de rayon r , de longueur l , sous l’action d’une différence de pression P entre les extrémités du tube, s’exprime par la relation:

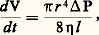où la constante 兀, qui s’exprime en poises (P), est le coefficient de viscosité du liquide (tabl. 1).

L’analyse de l’écoulement visqueux (appelé aussi laminaire) montre que la vitesse

d’écoulement du liquide varie de la périphérie au centre d’une section droite du tube. Elle est nulle à la périphérie et maximale au centre. Si l’on décompose le liquide en une multitude de couches concentriques à partir de la paroi, il apparaît que la viscosité traduit la résistance qui s’oppose au déplacement relatif d’une couche par rapport à sa voisine. On comprend ainsi que la viscosité d’un liquide est d’autant plus élevée que les molécules qui le composent sont plus grosses, ou que les interactions entre molécules sont plus fortes; que la viscosité décroît lorsque la température s’élève.

D’une façon assez paradoxale, on comprend l’importance de la viscosité dans les phénomènes de lubrification. En effet, si l’on se rapporte à ce qui a été dit du mouvement relatif d’un liquide et d’une surface solide, il apparaît qu’une pièce en mouvement dans un milieu liquide communique son mouvement aux couches de liquide proches de sa surface. Imaginons la surface cylindrique d’un axe qui tourne dans un palier. Les contraintes extérieures font qu’en l’absence de lubrifiant à tout moment l’axe et le palier sont en contact le long d’une génératrice du cylindre. En présence d’un lubrifiant, l’axe en rotation entraîne avec lui un film de liquide, lequel est capable de subsister malgré la pression extérieure qui tend à réduire son épaisseur dans la zone où les deux pièces sont pratiquement en contact. De l’analyse des forces en présence, on conclut aisément que le film résiduel est d’autant plus épais que le liquide est plus visqueux. Cependant, il est évident que la viscosité n’est pas le seul facteur important et que les propriétés de l’interface métal-liquide jouent également un rôle.

La tension superficielle des liquides et la capillarité

De nombreux phénomènes de la vie courante montrent qu’il faut dépenser de l’énergie pour augmenter la surface libre d’un liquide. On nomme tension superficielle le facteur de proportionnalité 塚 (tabl. 2) qui relie le travail dépensé à l’accroissement de la surface. Ainsi, c’est la tension superficielle qui fait que la goutte qui se forme à l’extrémité d’un compte-gouttes ne tombe que lorsqu’elle a atteint une masse suffisante pour vaincre les forces qui tendent à faire rentrer le liquide dans le tube pour en réduire la surface libre.

Les manifestations les plus importantes de la tension superficielle sont les phénomènes capillaires. Il est facile de vérifier que si un récipient contient un liquide quelconque (par exemple de l’eau) avec une très grande surface libre, et que l’on plonge dans le liquide l’une des extrémités d’un tube transparent (par exemple du verre) en maintenant le tube vertical, le niveau du liquide dans le tube est différent du niveau dans le récipient. En général, le liquide s’élève dans le tube au-dessus de la surface libre dans le récipient. Une observation attentive montre que la surface du liquide dans le tube a la forme d’un ménisque concave et que, d’une façon générale, l’angle de contact du liquide avec une surface verticale n’est pas droit. L’analyse du phénomène met en évidence le rôle de la tension superficielle ainsi que de la mouillabilité de la paroi du tube par le liquide, qui définit l’angle de contact . La dénivellation h du liquide dans le tube, comptée positivement vers le haut, s’exprime par la relation:

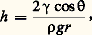où 福 est la masse spécifique du liquide (on suppose que celle de l’air est négligeable), r le rayon du tube et g l’accélération de la pesanteur. Lorsque le liquide mouille parfaitement la surface ( = 0), le liquide s’élève dans le tube et h peut prendre des valeurs très importantes. Par exemple, dans un tube de 2 micromètres de diamètre, de l’eau à la température ordinaire peut s’élever de plus de 15 mètres. Lorsque le liquide ne mouille pas la surface (c’est le cas du mercure avec le verre), le phénomène se produit en sens inverse. La capillarité est mise à profit dans de nombreuses applications, comme la mèche de la lampe à pétrole ou le bac à plantes à réserve d’eau.

3. La structure des liquides à l’échelle moléculaire

La fonction de distribution de paire

La diffusion des rayonnements de courte longueur d’onde, rayons X ou neutrons, révèle que les liquides se caractérisent par un certain ordre à courte distance mais sont désordonnés à longue distance. Dans le cas d’un liquide formé de particules sphériques (atomes, molécules), la seule variable géométrique servant à décrire le système est la distance r entre les centres des particules. La structure du liquide est décrite par une fonction de distribution de paire g (r ) qui permet de définir la probabilité de trouver une deuxième particule à une distance r de la première. Ainsi, si l’on prend comme origine le centre d’une particule et que l’on considère deux sphères de rayons r et r + dr centrées en ce point, le nombre moyen de particules ayant leur centre entre ces deux sphères est de:

où N est le nombre moyen de particules contenu dans un volume V de liquide. Dans le cas de liquides dont les molécules ont une forme non sphérique, on doit, outre la distance r , considérer des variables angulaires définissant l’orientation relative des deux molécules. Il est cependant toujours possible de définir une fonction g (r ) qui représente une moyenne sur toutes les orientations. Ainsi, dans tous les cas, la fonction de distribution de paire a la forme donnée par la figure 2. À grande distance, elle tend vers 1, ce qui signifie que le liquide est représenté par la densité moyenne de particules N/V. À très courte distance, g (r ) est évidemment nulle, puis passe par un maximum très marqué pour une distance r ⁰ qui représente la distance moyenne entre les centres de deux molécules voisines.

La fonction de distribution de paire est obtenue expérimentalement à partir de l’analyse de la variation angulaire de l’intensité de rayons X diffusée. Elle permet le calcul de nombreuses propriétés du liquide. On peut en particulier démontrer que la compressibilité isotherme 﨑^T obéit à l’équation: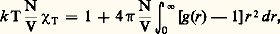

où k est la constante de Boltzmann et T la température absolue.

Les potentiels intermoléculaires et les modèles de l’état liquide

Pour comprendre théoriquement l’état liquide, il convient d’avoir en mémoire qu’il existe toujours entre deux molécules neutres des forces présentant un caractère attractif à courte distance, que l’on nomme forces de Van der Waals. Elles se manifestent par un minimum de la courbe de variation de l’énergie d’interaction u (r ) avec la distance. Dans le cas le plus simple, celui de deux atomes de gaz rare, l’énergie d’interaction ne dépend que de la distance, et sa variation est donnée par l’équation empirique de Lennard-Jones (fig. 3 a). Pour des systèmes plus complexes, d’autres phénomènes peuvent venir s’ajouter aux précédents pour modifier fortement la forme de la courbe u (r ) ci-contre (fig. 3 b). On retrouve cependant le minimum très marqué aux courtes distances interatomiques.

L’énergie d’interaction qui existe entre les particules d’un liquide permet d’en comprendre qualitativement les propriétés. Tout d’abord, elle explique la présence des phases liquide et solide à des températures supérieures au zéro absolu où, en son absence, l’agitation thermique serait suffisante pour donner immédiatement l’état gazeux. Elle permet également de comprendre le phénomène de tension superficielle des liquides. En effet, l’énergie d’interaction conduit chaque molécule à chercher à s’entourer du plus grand nombre de voisines, le liquide a donc tendance à présenter la surface libre le plus petite possible.

Du point de vue quantitatif, si l’on suppose que l’énergie d’interaction de n molécules peut se décomposer en une somme des énergies d’interaction de paire (ce qui n’est pas tout à fait vrai), la connaissance de u (r ) et de g (r ) permet de décrire complètement le liquide du point de vue thermodynamique. À titre d’exemple, l’énergie interne vaut, pour un liquide monoatomique:

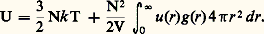Le premier terme de cette somme représentant la contribution de l’agitation thermique est le même que dans les gaz parfaits; le second est la valeur moyenne de l’énergie d’interaction des molécules.

Les méthodes de la chimie quantique permettent de déterminer théoriquement u (r ) pour des molécules de petite taille. En revanche, le calcul analytique de g (r ), qui s’effectue à partir de u (r ), n’est possible qu’au prix de nombreuses hypothèses simplificatrices. On préfère donc déterminer numériquement g (r ) au moyen de méthodes statistiques qui ne sont possibles que grâce à l’informatique (méthode de simulation de Monte-Carlo ). En fait, on s’est aperçu que la forme de l’énergie d’interaction ne joue pas un rôle très important dans la détermination de g (r ), qui dépend surtout de la valeur de r à laquelle l’énergie d’interaction croît brusquement par suite des forces de répulsion à courte distance. On est ainsi amené, en première approximation, à représenter un liquide monoatomique (comme l’argon) par un ensemble de sphères dures de diamètre 靖, dont le potentiel d’interaction est donné par la figure 3 c. Dans ce cas, une figure agrandie d’un liquide est constituée par un ensemble de nombreuses billes disposées sans ordre dans un récipient. On peut mesurer la densité d’un tel arrangement lorsqu’il est tassé au maximum et la comparer à celle que l’on aurait si les billes étaient arrangées régulièrement, comme le sont les atomes d’argon à l’état solide. La première densité est inférieure de 14 p. 100 à la seconde, ce qui représente justement la diminution de densité des gaz rares lors de la fusion. L’analogie peut être poussée plus loin et permet de calculer la fonction de distribution de paire d’un arrangement désordonné de billes. Les points calculés (fig. 2) sont très proches de la courbe expérimentale.

Dans la réalité, peu de molécules ont une forme qui se rapproche d’une sphère. La plupart du temps, les molécules sont déformables et, lorsqu’elles comportent une partie rigide, celle-ci a plutôt la forme soit d’un bâtonnet soit d’une plaquette plus ou moins allongée. Dans ce dernier cas, on comprend que, même en l’absence de forces intermoléculaires, des entités anisotropes tendent à s’orienter parallèlement les unes aux autres comme le font des grains de riz ou des pièces de monnaie dans un récipient. Cela est encore plus marqué entre deux molécules que les forces de Van der Waals tendent à les rapprocher au maximum. Dans le cas de molécules particulièrement anisotropes, il arrive que, à la fusion du cristal (phase ordonnée), on obtienne un liquide dont les molécules, libres de se mouvoir en translation, demeurent sensiblement parallèles les unes aux autres. Ces liquides ont des propriétés optiques comparables à celles de certains cristaux: on parle alors de cristaux liquides. Ce n’est qu’à une température supérieure au point de fusion que sous l’effet de l’agitation thermique le système passe à l’état de liquide isotrope, où les molécules ont des orientations au hasard. Le passage d’une phase cristal liquide à un liquide isotrope se fait à une température fixée, tout comme la fusion normale. L’analyse de la structure des cristaux liquides a amené à distinguer trois phases que l’on nomme: smectique; nématique; cholestérique. Un même composé peut présenter plusieurs phases cristal liquide différentes entre le point de fusion et le point de transition à l’état liquide normal.

Ces phases ont la particularité de s’orienter dans un champ électrique, et certaines d’entre elles réfléchissent différemment la lumière selon leur orientation. C’est le principe des dispositifs d’affichage à cristaux liquides où le champ électrique est créé entre une fenêtre de verre conducteur et une mosaïque de plaques pouvant être portées à un potentiel électrique différent de la fenêtre pour dessiner une lettre ou un chiffre ^{[cf. CRISTAUX LIQUIDES]}.

On peut également rencontrer un potentiel intermoléculaire très anisotrope lorsque les deux molécules peuvent établir entre elles des liaisons chimiques faibles mais dirigées. Elles sont connues sous le nom de liaisons hydrogène, comme celles qui se forment entre deux molécules d’eau voisines (cf. EAU - Physicochimie). Ces liaisons intermoléculaires imposent à la glace une structure très lacunaire. Leur rupture partielle à la fusion provoque l’augmentation de masse spécifique caractéristique de l’eau. Lorsque la température continue à s’élever, la rupture de nouvelles liaisons tend à faire augmenter la densité, alors que l’agitation thermique provoque l’effet contraire. On comprend ainsi les anomalies dans le coefficient de dilatation de l’eau au-dessus du point de fusion et son maximum de densité à 4 ⁰C. Ces mêmes forces intermoléculaires expliquent la tension superficielle et la viscosité de l’eau qui sont toutes deux anormalement élevées pour une molécule de petite taille.

La dynamique des liquides

La dynamique de la réponse d’un liquide à un déplacement d’équilibre est généralement traduite par un coefficient dit de transport, comme les coefficients de viscosité, de diffusion, de conductibilité thermique, etc. Ces grandeurs sont liées à des fluctuations de structure dans le temps autour de la structure moyenne décrite précédemment. Ainsi, le coefficient de diffusion peut être relié au rapport du temps moyen que met une molécule pour passer d’un site à un autre au temps moyen de résidence dans un site.

Encyclopédie Universelle. 2012.